动态规划
非动态规划专栏
最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
示例 1:
1
2
3
| 输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public int maxSubArray(int[] nums) {
if (nums.length == 1) {
return nums[0];
}
int dp[] = new int[nums.length];
dp[0] = nums[0];
int res = dp[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
res = Math.max(res, dp[i]);
}
return res;
}
}
|
跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说,如果你在索引 i 处,你可以跳转到任意 (i + j) 处:
0 <= j <= nums[i] 且i + j < n
返回到达 n - 1 的最小跳跃次数。测试用例保证可以到达 n - 1。
示例 1:
1
2
3
4
| 输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int jump(int[] nums) {
int dp[] = new int[nums.length];
Arrays.fill(dp, 1000000);
dp[0] = 0;
for (int i = 1; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (j + nums[j] >= i) {
dp[i] = Math.min(dp[i], dp[j] + 1);
}
}
}
return dp[nums.length - 1];
}
}
|
爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public int climbStairs(int n) {
if (n <= 2) {
return n;
}
int dp[] = new int[n + 1];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}
|
杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
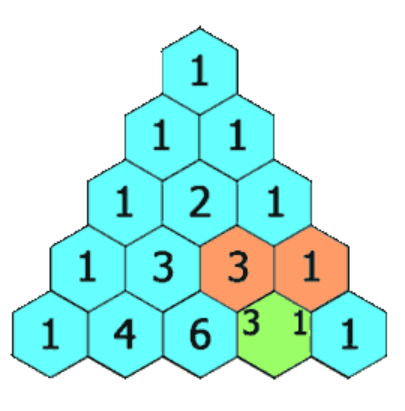
示例 1:
1
2
| 输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res=new ArrayList<>();
for(int i=0;i<numRows;i++){
List<Integer> list=new ArrayList<>();
for(int j=0;j<=i;j++){
if(j==0||j==i){
list.add(1);
}else{
list.add(res.get(i-1).get(j-1)+res.get(i-1).get(j));
}
}
res.add(list);
}
return res;
}
}
|
打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
1
2
3
4
| 输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public int rob(int[] nums) {
if (nums.length == 0) {
return 0;
}
if (nums.length == 1) {
return nums[0];
}
int dp[] = new int[nums.length];
dp[0] = nums[0];
dp[1] = Math.max(dp[0], nums[1]);
for (int i = 2; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1], nums[i] + dp[i - 2]);
}
return dp[nums.length - 1];
}
}
|
完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
1
2
3
| 输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
|
示例 2:
1
2
3
| 输入:n = 13
输出:2
解释:13 = 4 + 9
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public int numSquares(int n) {
int dp[] = new int[n + 1];
for(int i=0;i<=n;i++){
dp[i]=i;
}
for (int i = 0; i <= n; i++) {
for (int j = 0; j < i; j++) {
if ((i - j * j) >= 0) {
dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
}
}
}
return dp[n];
}
}
|
零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
1
2
3
| 输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
|
解法1:dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int coinChange(int[] coins, int amount) {
int dp[]=new int[amount+1];
Arrays.fill(dp,Integer.MAX_VALUE-100);
dp[0]=0;
for(int i=1;i<=amount;i++){
for(int coin:coins){
if((i-coin)>=0)
dp[i]=Math.min(dp[i],dp[i-coin]+1);
}
}
return dp[amount]==Integer.MAX_VALUE-100?-1:dp[amount];
}
}
|
解法2:回溯
参考组合总和,那个是求出所有总和,这个是求组合的元素最小个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
private int pdmin = Integer.MAX_VALUE;
public int coinChange(int[] coins, int amount) {
List<Integer> cur = new ArrayList<>();
huisu(coins, amount, cur, 0, 0);
return pdmin == Integer.MAX_VALUE ? -1 : pdmin;
}
public void huisu(int[] coins, int amount, List<Integer> cur, int sum, int index) {
if (sum == amount) {
pdmin = Math.min(pdmin, cur.size());
return;
}
if (sum > amount) {
return;
}
for (int i = index; i < coins.length; i++) {
cur.add(coins[i]);
huisu(coins, amount, cur, sum + coins[i], i);
cur.remove(cur.size() - 1);
}
}
}
|
单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
1
2
3
| 输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
boolean dp[] = new boolean[s.length() + 1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
dp[i] |= dp[j] && wordDict.contains(s.substring(j, i));
}
}
return dp[s.length()];
}
}
|
最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
1
2
3
| 输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
|
示例 2:
1
2
| 输入:nums = [0,1,0,3,2,3]
输出:4
|
示例 3:
1
2
| 输入:nums = [7,7,7,7,7,7,7]
输出:1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public int lengthOfLIS(int[] nums) {
int dp[] = new int[nums.length];
Arrays.fill(dp, 1);
int max = dp[0];
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]) {
dp[i] = Math.max(dp[j] + 1, dp[i]);
}
}
max = Math.max(max, dp[i]);
}
return max;
}
}
|
乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续 子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
示例 1:
1
2
3
| 输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
|
示例 2:
1
2
3
| 输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public int maxProduct(int[] nums) {
int dpMax[] = new int[nums.length];
int dpMin[] = new int[nums.length];
dpMax[0] = dpMin[0] = nums[0];
int res = dpMax[0];
for (int i = 1; i < nums.length; i++) {
dpMax[i] = Math.max(Math.max(nums[i] * dpMax[i - 1], nums[i] * dpMin[i - 1]), nums[i]);
dpMin[i] = Math.min(Math.min(nums[i] * dpMax[i - 1], nums[i] * dpMin[i - 1]), nums[i]);
res = Math.max(res, dpMax[i]);
}
return res;
}
}
|
分割等和子集(待学习)
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
1
2
3
| 输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
|
示例 2:
1
2
3
| 输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
|
用回溯会超时
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public boolean canPartition(int[] nums) {
int sum = Arrays.stream(nums).sum();
if (sum % 2 == 1) {
return false;
}
int target = sum / 2;
List<List<Integer>> res = new ArrayList<>();
List<Integer> cur = new ArrayList<>();
huisu(res, nums, cur, target, 0, 0);
return res.size() != 0;
}
public void huisu(List<List<Integer>> res, int nums[], List<Integer> cur, int target, int sum, int index) {
if (sum == target) {
res.add(new ArrayList<>(cur));
return;
}
if (sum > target || index >= nums.length) {
return;
}
huisu(res, nums, cur, target, sum, index + 1);
cur.add(nums[index]);
huisu(res, nums, cur, target, sum + nums[index], index + 1);
cur.remove(cur.size() - 1);
}
}
|
最长有效括号(非DP)
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号 子串 的长度。
左右括号匹配,即每个左括号都有对应的右括号将其闭合的字符串是格式正确的,比如 "(()())"。
示例 1:
1
2
3
| 输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
|
示例 2:
1
2
3
| 输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public int longestValidParentheses(String s) {
Stack<Integer> stack = new Stack<>();
stack.push(-1);
int max = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else {
stack.pop();
if (stack.isEmpty()) {
stack.push(i);
} else {
max = Math.max(max, i - stack.peek());
}
}
}
return max;
}
}
|
二维动态规划
不同路径
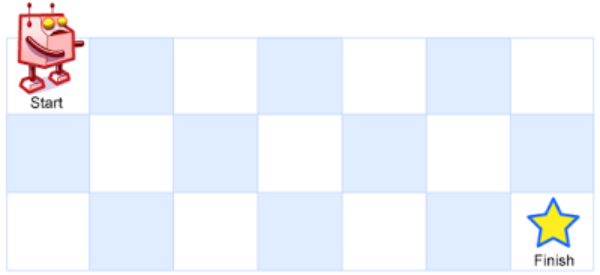
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public int uniquePaths(int m, int n) {
int dp[][]=new int[m][n];
for(int i=0;i<n;i++){
dp[0][i]=1;
}
for(int i=0;i<m;i++){
dp[i][0]=1;
}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
dp[i][j]=dp[i][j-1]+dp[i-1][j];
}
}
return dp[m-1][n-1];
}
}
|
最小路径和
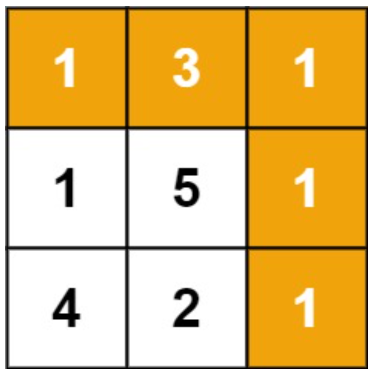
给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
1
2
3
| 输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
|
示例 2:
1
2
| 输入:grid = [[1,2,3],[4,5,6]]
输出:12
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int dp[][] = new int[m][n];
dp[0][0] = grid[0][0];
for (int i = 1; i < n; i++) {
dp[0][i] = dp[0][i - 1] + grid[0][i];
}
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.min(dp[i - 1][j] + grid[i][j], dp[i][j - 1] + grid[i][j]);
}
}
return dp[m - 1][n - 1];
}
}
|
最长回文子串
给你一个字符串 s,找到 s 中最长的 回文 子串。
示例 1:
1
2
3
| 输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
|
示例 2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| class Solution {
public String longestPalindrome(String s) {
if (s == null || s.length() < 2)
return s;
int n = s.length();
boolean[][] dp = new boolean[n][n];
int start = 0;
int maxLen = 1;
for (int i = 0; i < n; i++) {
dp[i][i] = true;
}
for (int i = 0; i < n - 1; i++) {
if (s.charAt(i) == s.charAt(i + 1)) {
dp[i][i + 1] = true;
start = i;
maxLen = 2;
}
}
for (int len = 3; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
int j = i + len - 1;
if (s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]) {
dp[i][j] = true;
start = i;
maxLen = len;
}
}
}
return s.substring(start, start + maxLen);
}
}
|
最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
1
2
3
| 输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
|
示例 2:
1
2
3
| 输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length();
int n = text2.length();
int dp[][] = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
}
|
编辑距离
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
示例 1:
1
2
3
4
5
6
| 输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length();
int n = word2.length();
int dp[][] = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
dp[i][0] = i;
}
for (int i = 0; i <= n; i++) {
dp[0][i] = i;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + 1);
}
}
}
return dp[m][n];
}
}
|
总结:












