Sorry, your browser cannot access this site
This page requires browser support (enable) JavaScript
Learn more >

回溯

发布于：Aug 9, 2025

回溯

全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

解题思路：回溯算法

全排列问题的核心思想是回溯，我们可以把这个过程想象成：

  1. 从数组中选择一个数字放在第一位
  2. 从剩余数字中选择一个放在第二位
  3. 继续这个过程直到所有位置都填满
  4. 如果当前路径不满足条件，就回退到上一步，尝试其他选择

具体点：

  • 通过交换元素位置来生成排列
  • 每次将待排列的元素与当前位置index交换
  • 递归处理后续位置
  • 回溯时再次交换回来
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        huisu(nums, 0, res);
        return res;

    }

    public void huisu(int[] nums, int index, List<List<Integer>> res) {
        if (index == nums.length) {
            List<Integer> list = new ArrayList<>();
            for (int num : nums) {
                list.add(num);

            }
            res.add(list);
            return;
        }

        for (int i = index; i < nums.length; i++) {
            swap(nums, index, i);
            huisu(nums, index + 1, res);
            swap(nums, index, i);
        }

    }

    public void swap(int nums[], int i, int j) {
        int temp = nums[j];
        nums[j] = nums[i];
        nums[i] = temp;
    }

}

子集

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

思路1：二进制。

长度为n的数组子集个数的2ⁿ， 每个元素有两种状态：选择(1) 或不选择(0)，这正好对应二进制！

对于数组 [1, 2, 3]：

  • 二进制 000 → 都不选 → []
  • 二进制 001 → 选第0个 → [1]
  • 二进制 010 → 选第1个 → [2]
  • 二进制 011 → 选第0,1个 → [1, 2]
  • 二进制 100 → 选第2个 → [3]
  • 二进制 101 → 选第0,2个 → [1, 3]
  • 二进制 110 → 选第1,2个 → [2, 3]
  • 二进制 111 → 都选 → [1, 2, 3]

总结：

  • n个元素有2ⁿ个子集
  • 用0到2ⁿ-1的所有整数来表示，即1<<n,for (int i = 0; i < (1 << n); i++)
  • 然后判断这些整数的每一位是否是1，如果是1则加到list里面去；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        int n = nums.length;
        int count = 1 << n;
        List<List<Integer>> res = new ArrayList<>();

        for (int i = 0; i < count; i++) {
            List<Integer> list = new ArrayList<>();
            for (int j = 0; j < n; j++) {

                if (((i >> j) & 1) == 1) {
                    list.add(nums[n - j - 1]);

                }
            }
            res.add(list);
        }
        return res;

    }

}

思路2：迭代法

核心思想：逐个添加元素。

关键洞察： 每次添加一个新元素时，新的子集 = 原有的所有子集 + 原有的所有子集都加上新元素。

初始状态：

1
result = [[]]  // 只有空集

第1步：添加元素1

1
2
3
4
5
当前result = [[]]
对每个已有子集，生成包含1的新版本：
[] → [] + [1]

result = [[], [1]]

第2步：添加元素2

1
2
3
4
5
6
当前result = [[], [1]]
对每个已有子集，生成包含2的新版本：
[] → [] + [2]
[1] → [1] + [1,2]

result = [[], [1], [2], [1,2]]

第3步：添加元素3

1
2
3
4
5
6
7
8
当前result = [[], [1], [2], [1,2]]
对每个已有子集，生成包含3的新版本：
[] → [] + [3]
[1] → [1] + [1,3]
[2] → [2] + [2,3]
[1,2] → [1,2] + [1,2,3]

最终result = [[], [1], [2], [1,2], [3], [1,3], [2,3], [1,2,3]]

每一步的子集数量都会复制一倍：1 → 2 → 4 → 8

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
       
        List<List<Integer>> res = new ArrayList<>();
        int n = nums.length;
        List<Integer> cur = new ArrayList<>();
        res.add(cur);
        for (int i = 0; i < n; i++) {
            int size = res.size();//要注意，不能使用j <  res.size()，不然里面的size一直在变
            for (int j = 0; j < size; j++) {
                List<Integer> temp = new ArrayList<>(res.get(j));//注意这里，不是直接res.get(j),要拷贝一份
                temp.add(nums[i]);
                res.add(temp);
            }
        }

        return res;
    }
}

思路3：递归回溯。

每一个元素都有两个选择，我要这个元素、我不要这个元素。

核心思想： 对于每个元素，我们都有两个选择：

  1. 选择这个元素加入当前子集
  2. 不选择这个元素

具体过程：

  1. 从第一个元素开始
  2. 对每个元素做决定：要它还是不要它
  3. 每做一次决定，就递归处理下一个元素
  4. 当处理完所有元素时，得到一个完整的子集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public List<List<Integer>> subsets(int[] nums) {

        List<List<Integer>> res = new ArrayList<>();
        List<Integer> cur = new ArrayList<>();
        huisu(res, cur, 0, nums);
        return res;

    }

    public void huisu(List<List<Integer>> res, List<Integer> cur, int index, int[] nums) {
        if (index == nums.length) {
            res.add(new ArrayList<>(cur));
            return;
        }
        //不要这个元素就直接跳
        huisu(res, cur, index + 1, nums);
		//要这个元素就添加了再回溯
        cur.add(nums[index]);
	
        huisu(res, cur, index + 1, nums);

        cur.remove(cur.size() - 1);

    }
}

电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

image-20250808221017575

示例 1：

1
2
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

解法1：队列

核心思想：使用队列按层处理，每处理一个数字就生成一层新的组合。

具体步骤（以 digits = "23" 为例）：

  1. 初始化

    ：创建一个队列，放入空字符串 

    1
    ""
    • 队列状态：[""]

  2. 处理第一个数字 ‘2’

    ：

    • 出队空字符串 ""
    • 将 ‘2’ 对应的每个字母（’a’, ‘b’, ‘c’）分别加到空字符串后面
    • 新组合 "a", "b", "c" 依次入队
    • 队列状态：["a", "b", "c"]

  3. 处理第二个数字 ‘3’

    ：

    • 出队 "a"，加上 ‘3’ 对应的字母（’d’, ‘e’, ‘f’），得到 "ad", "ae", "af" 入队 队列状态：["b", "c", "ad", "ae", "af"]
    • 出队 "b"，加上 ‘3’ 对应的字母，得到 "bd", "be", "bf" 入队
      队列状态：["c", "ad", "ae", "af", "bd", "be", "bf"]
    • 出队 "c"，加上 ‘3’ 对应的字母，得到 "cd", "ce", "cf" 入队 队列状态：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]

  4. 结束：所有数字处理完毕，队列中的元素就是所有可能的字母组合。

关键点：每处理一个数字，就要把当前队列中的所有元素都出队一遍，然后生成新的组合入队。这样可以确保每一层的组合都能与下一个数字的所有字母结合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {

    public List<String> letterCombinations(String digits) {
        if (digits.length() == 0) {
            return new ArrayList<>();
        }
        Queue<String> queue = new LinkedList<>();
        queue.add("");
        String map[] = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
        for (int i = 0; i < digits.length(); i++) {
            int index = digits.charAt(i) - '0';
            String str = map[index];
            int n = queue.size();
            for (int j = 0; j < n; j++) {
                String temp = queue.poll();
                for (char ch : str.toCharArray()) {

                    queue.add(temp + ch);
                }
            }
        }
        // b c ad ae af
        return new ArrayList<>(queue);

    }

}

解法2：回溯法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {

    public List<String> letterCombinations(String digits) {
        if (digits.length() == 0) {
            return new ArrayList<>();
        }
        String map[] = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
        List<String> res = new ArrayList<>();
        List<Character> cur = new ArrayList<>();
        huisu(res, digits, cur, 0, map);
        return res;
    }

    public void huisu(List<String> res, String digits, List<Character> cur, int index, String map[]) {
        if (index == digits.length()) {
            StringBuilder sb = new StringBuilder();
            for (char ch : cur) {
                sb.append(ch);
            }
            res.add(sb.toString());
            return;
        }
        String str = map[digits.charAt(index) - '0'];
        for (int i = 0; i < str.length(); i++) {
            cur.add(str.charAt(i));
            huisu(res, digits, cur, index + 1, map);
            cur.remove(cur.size() - 1);
        }
    }

}

组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

1
2
3
4
5
6
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

关键步骤总结

  1. 检查答案：if (sum == target) - 凑够了就是答案
  2. 检查超限：if (sum > target) - 加多了就退出
  3. 做选择：current.add(candidates[i]) - 放进篮子
  4. 递归：backtrack(..., i, ...) - 继续凑，可以重复选
  5. 撤销：current.remove(...) - 拿出来，试试别的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> cur = new ArrayList<>();
        huisu(candidates, res, cur, 0, target, 0);
        return res;
    }

    public void huisu(int[] candidates, List<List<Integer>> res, List<Integer> cur, int index, int target, int sum) {
        if (sum == target) {
            res.add(new ArrayList<>(cur));
            return;
        }
        if (sum > target) {
            return;
        }
        for (int i = index; i < candidates.length; i++) {
            cur.add(candidates[i]);
            huisu(candidates, res, cur, i, target, sum + candidates[i]);
            cur.remove(cur.size() - 1);
        }
    }

}

括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

1
2
输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

解题思路

两段回溯

有效括号的规则：

  1. 左括号数量 = 右括号数量 = n

  2. 在任意位置，左括号数量 ≥ 右括号数量（不能出现)(这种情况）

  3. 左括号剪枝：if (left< n) - 左括号不能超过n个

  4. 右括号剪枝：if (right< lef) - 右括号不能超过左括号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<>();
        List<Character> cur = new ArrayList<>();
        huisu(n, cur, res, 0, 0);
        return res;
    }

    public void huisu(int n, List<Character> cur, List<String> res, int left, int right) {
        // 基础情况：当前路径长度等于2n，说明生成了完整的括号组合
        if (cur.size() == n * 2) {
            // 将List<Character>转换为String
            StringBuilder sb = new StringBuilder();
            for (char ch : cur) {
                sb.append(ch);
            }
            res.add(sb.toString()); // 将当前有效组合加入结果集
            return;
        }

        // 选择1：添加左括号
        // 剪枝条件：左括号数量不能超过n
        if (left < n) {
            cur.add('('); // 第1步：做选择 - 添加左括号到当前路径
            huisu(n, cur, res, left + 1, right); // 第2步：递归 - 左括号数量+1，继续构建
            cur.remove(cur.size() - 1); // 第3步：撤销选择 - 回溯，移除刚才添加的左括号
        }

        // 选择2：添加右括号
        // 剪枝条件：右括号数量不能超过当前的左括号数量（保证括号有效）
        if (right < left) {
            cur.add(')'); // 第1步：做选择 - 添加右括号到当前路径
            huisu(n, cur, res, left, right + 1); // 第2步：递归 - 右括号数量+1，继续构建
            cur.remove(cur.size() - 1); // 第3步：撤销选择 - 回溯，移除刚才添加的右括号
        }
    }
}

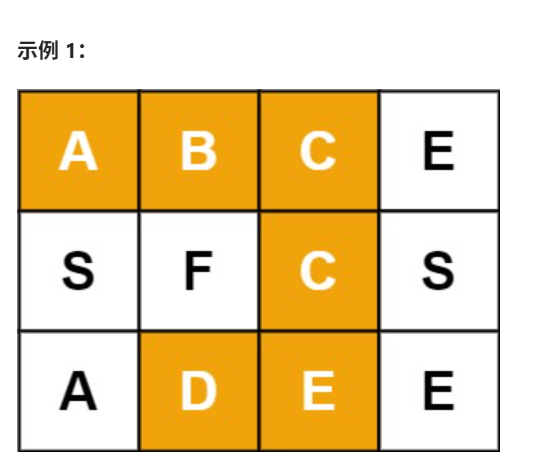
单词搜索

image-20250808234308887

1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

解法：

这是一个典型的二维网格回溯问题：

  1. 遍历每个起点：找到单词第一个字母的位置作为起点
  2. 四方向搜索：从起点向上下左右四个方向搜索下一个字母
  3. 标记访问状态：提前保持好字母，然后用#标记数组避免重复使用同一个格子
  4. 回溯：如果当前路径不行，撤销标记#，尝试其他路径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public boolean exist(char[][] board, String word) {
        int m = board.length;
        int n = board[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (huisu(board, i, j, word, 0, m, n)) {//注意这里不能直接return huisu，只要true才能return，如果直接return的话后面有成功的就被抛弃了
                    return true;
                }
            }
        }
        return false;
    }

    public boolean huisu(char[][] board, int i, int j, String word, int index, int m, int n) {
        // 找到完整单词
        if (index == word.length()) {
            return true;
        }
        // 边界和条件检查
        if (i < 0 || i > m - 1 ||
                j < 0 || j > n - 1 ||
                board[i][j] != word.charAt(index)) {
            return false;
        }
        // 第1步：做选择 - 暂存当前字符并标记为已访问
        char temp = board[i][j];// 用特殊字符标记已访问
        board[i][j] = '#';
        // 第2步：递归 - 四方向搜索，只要找到一个方向就算成功
        boolean isTrue = huisu(board, i + 1, j, word, index + 1, m, n) ||
                huisu(board, i - 1, j, word, index + 1, m, n) ||
                huisu(board, i, j + 1, word, index + 1, m, n) ||
                huisu(board, i, j - 1, word, index + 1, m, n);
        if (isTrue == true) {
            return true;
        }
        // 第3步：撤销选择 - 恢复原字符
        board[i][j] = temp;
        return false;
    }

}

分割回文串

给你一个字符串 s，请你将 s 分割成一些 子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

示例 1：

1
2
输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

解法：

基本流程：

  1. 选择分割点：在每个位置尝试分割字符串
  2. 验证回文：检查分割出的子串是否为回文
  3. 递归继续：如果是回文，继续分割剩余字符串
  4. 回溯尝试：如果当前分割不行，撤销选择，尝试其他分割点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public List<List<String>> partition(String s) {
        List<List<String>> res = new ArrayList<>();
        List<String> cur = new ArrayList<>();
        huisu(res, s, cur, 0);
        return res;
    }

    public void huisu(List<List<String>> res, String s, List<String> cur, int index) {
        // 基础情况：已经处理完整个字符串
        if (index == s.length()) {
            res.add(new ArrayList<>(cur));
            return;
        }
        // 尝试每个可能的分割点
        for (int i = index; i < s.length(); i++) {

            // 提取子串[start, end]
            String str = s.substring(index, i + 1);
            // 如果当前子串是回文，则可以作为一个分割
            if (isHui(str)) {
                cur.add(str);
                huisu(res, s, cur, i + 1);//这里如果不知道是i+1还是index+1，直接试一试
                cur.remove(cur.size() - 1);
            }
        }
    }

    //判断回文
    public boolean isHui(String s) {
        int i = 0;
        int j = s.length() - 1;
        while (i < j) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
            i++;
            j--;
        }
        return true;
    }
}

总结

一共7题，全排列、子集、电话号码、组合总数、括号生成、(网格)单词搜索、分割回文串。

全排列：这里没有用到cur，是通过交换元素位置，达到条件后，nums里面就是要收集的。

子集：有三种方法，二进制、从空集开始新增元素、回溯。这里的回溯没有用到for。

电话号码：1是可以用队列，而是用回溯。

组合总数：在一个集合里选择几个数字的和=target，也适用于零钱兑换coins，他是找组合的最小值，但是会超时。

括号生成：也没用到for，根据左括号和右括号的数量来回溯的。

分割回文串：在for里面判断inde到i是否是子串才决定是否回溯

更新于：Aug 12, 2025

评论